How To Find The Surface Area Of A Triangle

Mark, a math enthusiast, loves writing tutorials for stumped students and those who need to castor upwards on their math skills.

What Is a Prism?

A prism is a three-dimensional object whose two finish faces are identical and whose sides are parallelograms (a four-sided shape with two pairs of parallel sides). The type of prism is determined by the shape of its ends. Hence, a prism with a triangle at each finish is called a triangular prism. It doesn't matter if that prism is right-angled or isosceles, the way nosotros discover the surface area is the same for both types.

How Do We Detect the Surface area?

The surface area of any prism is the total area of all its sides and faces. A triangular prism has three rectangular sides and two triangular faces. To find the expanse of the rectangular sides, use the formula A = lw, where A = expanse, fifty = length, and h = height. To find the area of the triangular faces, use the formula A = 1/2bh, where A = surface area, b = base, and h = height. Once you lot have the areas of all sides and faces, you merely add together them together to get the surface expanse.

how-to-work-out-the-surface-area-of-a-triangular-prism-right-angled-and-isosceles

Formulas You'll Need to Complete This Lesson


Shape	Formula
Area of a triangle	A = 1/2bh
Expanse of a rectangle	A = lw
Area of triangular prism	SA = bh + (s1 + s2 + s3)H

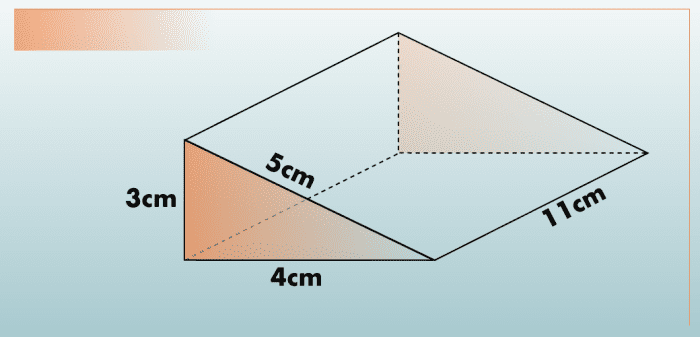
Example 1: Detect the Surface area of the Correct-Angled Triangular Prism To a higher place

Let'south begin with the triangular faces. Both faces accept the same expanse because they are congruent! Just multiply the base and height and split up the answer past 2:

Area of triangular faces

= 1/ii(base × height)
= 1/2(iii × 4) = six cm²

Side by side work out the expanse of the rectangular sides. Each side is a different size, and can be calculated by multiplying the length by the width:

Expanse of sloping rectangular side

= length x width
= xi x five
= 55 cm²

Area of back side

= xi ten iii
=33 cm²

Area of bottom side

= 11 x 4
= 44 cm²

Using a Formula to Discover the Surface Surface area

Now that nosotros've covered the nuts, it'due south time to introduce a less tedious method. In that location is a single formula y'all can utilize to calculate the surface area of a triangular prism:

SA = bh + (s1 + s2 + s3)H

In the above formula, b = the base and h = the height of the triangle, s1, s2, and s3 = the length of each side of the triangle, and H = the prism's pinnacle (which is the same as the rectangles' length).

Y'all might be wondering how we came up with this formula. Well, it'southward pretty unproblematic. If you'll recall, the surface surface area is institute by adding together the area of each side and face. Allow's start with the two triangles on the ends. The area of each triangle is 1/2bh. Since they are both identical, we can double this formula to find both of their areas at the same time.

The area of both triangles

= two(i/2bh)
= 2/2bh
= bh

Typically to work out the area of the 3 rectangular sides, you lot would multiply each i's length by its respective width. However, this isn't necessary because the sides of the triangles are equal to the widths of the three rectangles. Similarly, the prism's tiptop, H, is equal to the length of each rectangle. Therefore, multiplying the height, H, of the prism (length of the rectangles) by the perimeter (the three rectangular widths) of its base of operations volition requite u.s. the surface area of each rectangle.

The area of the rectangular sides

= (s1 + s2 + s3)H

Therefore, the expanse of a triangular prism

= the expanse of the triangular faces + the area of the rectangular sides
= bh + (s1 +s2 +s3)H

Instance 1.ane

Let's use our new formula to redo the case above!

The surface surface area

= bh + (s1 + s2 + s3)H
= 4(3) + (three + v + four)(eleven)
= 12 + 12(11)
= 12 + 132
= 144 cm²

As you can run into, our answer matches the one above. Now that we know our formula works, allow's put it to use in the next instance.

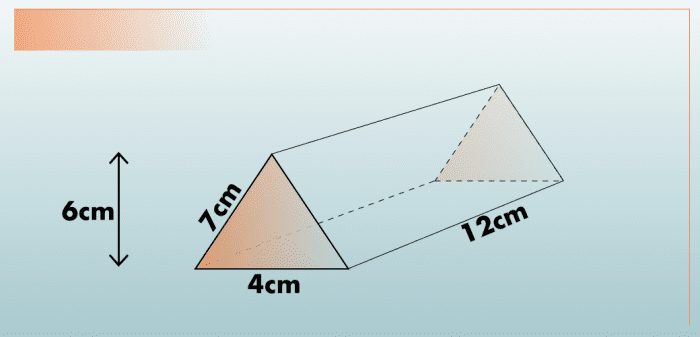
Example two: Notice the Surface Area of the Isosceles Triangular Prism Higher up

Outset, plug the known values into the equation.

SA = bh + (s1 + s2 + s3)H
SA = four(vi) + (4 + 7 + seven)(12)

Next, calculate the perimeter of the triangles (add together the iii sides), followed by their expanse (base times acme).

SA= 24 + 18(12)

Then, multiply the perimeter by the height of the prism.

SA = 24 + 216

Finally, add together the remaining values together to get your reply.

SA = 240 cm²

Instance ii.i: Let's Check Our Piece of work!

Our answers lucifer! Great job!
Triangular Face (TF1)	TF2	Rectangular Side i (RS1)	RS2	Rectangular Base	Total
A = one/2bh	A = 1/2bh	A = lw	A = lw	A = lw
A = 1/2(4 x 6)	A = ane/2(iv x half-dozen)	A = 12(7)	A = 12(7)	A = 12(iv)
A = 12	A = 12	A = 84	A = 84	A = 48
12 +	12 +	84 +	84 +	48 =	240 cm^two

Still Stumped? Hither's a Bully Tutorial on Calculating Surface Area Using a Net

Review Questions

I. Use the diagram below to solve the following problems.

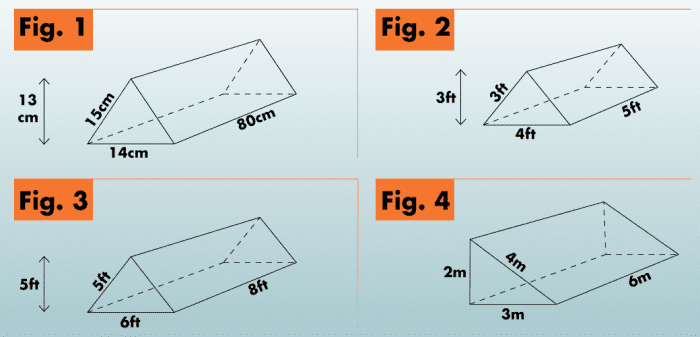
Alan wants to surprise his sister with a giant Toblerone for passing her math class (Fig. one). Alan needs to know the area of the Toblerone to buy the correct corporeality of wrapping paper. What is its surface surface area?
John just bought a brand new roof for his shed. Unfortunately, he hates that it's neon green. He would like to repaint his roof just doesn't know how much pigment he should buy. He is on a pretty tight upkeep. Using the image above (Fig. 2), discover the surface area of the roof (including the bottom).
Jackie wants to build a tent for her daughter. She has already constructed its frame but does not know how much textile she needs to cover it. Notice the area of the tent (Fig. iii) using the image higher up.
Katie'southward boss wants her to purchase concrete for the ramp that they are building. He gave her the blueprints, but she is even so stumped. Find the surface area of the image above (Fig. 4) so Katie doesn't lose her job.

Two. Find the surface expanse of the following:

A prism whose triangular ends have a height of 6 inches with a 4-inch base and each rectangular side is 5 inches long and six inches broad.
A prism whose triangular ends have a height of ten meters with a 5-meter base and each rectangular side is 4 meters long and 10 meters wide.
A prism whose triangular ends have a height of x inches with a fifteen-inch base and each rectangular side is 12 inches long and 10 inches broad.
A prism whose triangular ends take a summit of 6 meters with an 8-meter base of operations and each rectangular side is 15 meters long and 6 meters broad.

Answers

Section I

3,702 cmⁱⁱ
62 ftⁱⁱ
158 ft²
sixty one thousand²

Section 2

114 in^two
170 mⁱⁱ
510 inⁱⁱ
318 mⁱⁱ

Questions & Answers

Question: What is the formula for finding the Full Surface Expanse of a Prism?

Answer: It depends on the type of prism, so there isn't i formula which works for all.

Question: How do you lot notice the surface area of the right triangular prism with ii numbers?

Respond: You lot may need to apply Pythagoras on the triangular confront to work out a missing side length if you are only given 2 lengths to start off with.

Question: The base length of the triangular face is 5cm, the perpendicular height is 2.4cm and the length of the prism is 7, how to calculate the surface surface area of that triangular prism?

Respond: The area of the triangular face is v times 2.4 divided by 2 which is 6cm^ii.

The area of the triangular face at the dorsum of the prism is also 6cm^2.

The expanse of the rectangular bottom face is 5 times 7 which is 35cm^two.

The expanse of the rectangular vertical face up is 2.4 times 7 which is 16.8 cm^2.

Before y'all can work out the rectangular sloping face apply Pythagoras to give the other side length which will exist 5.5cm

And then the sloping rectangular face will be 5.v times vii which is 38.5 cm^2.

Calculation upwards these areas will give a final answer of 102.3 cm^2.

Question: How exercise you work out the surface area for a right-angled triangular prism?

Answer: Piece of work out the area of the triangles at the front and back of the prism, using 1/2 times base times height.

(These triangles will have the same area).

Side by side piece of work out the surface area of the iii rectangular faces of the prism using length times width for each rectangle.

Now add up the 5 areas to give the surface expanse of the triangular prism.

Question: How do I find the full surface surface area of a cube?

Respond: Work out the area of 1 of the square faces (length times width).

Then multiply this answer by 6, as there are six square faces which make the cube.

Question: How would you work out the surface expanse of a scalene triangle, and what if that is a prism?

Answer: It's very like to the correct-angled triangular prism. Work out the surface area of the two triangles at either terminate and then add on the area of the three rectangles around the center.